Рассмотрим некоторые соотношения, которые полезны при решении задач на шар, вписанный в конус.
В любой конус можно вписать шар. Вписанный в конус шар (или сфера, вписанная в конус) касается основания конуса в его центре, а боковой поверхности — по окружности. Центр шара (сферы) лежит на оси конуса.
При решении задач на шар, вписанный в конус, удобнее всего рассмотреть сечение комбинации тел плоскостью, проходящей через ось конуса и центр шара.
 Это сечение представляет собой равнобедренный треугольник, боковые стороны которого — образующие конуса, а основание — диаметр конуса. Вписанный в этот треугольник круг — большой круг шара (то есть круг, радиус которого равен радиусу шара).
Это сечение представляет собой равнобедренный треугольник, боковые стороны которого — образующие конуса, а основание — диаметр конуса. Вписанный в этот треугольник круг — большой круг шара (то есть круг, радиус которого равен радиусу шара).
Для данного рисунка образующие SA=SB=l, высота конуса SO=H, радиус вписанного шара OO1=O1F=R. Так как центр вписанного круга — точка пересечения биссектрис треугольника, то ∠OBO1=∠FBO1, OB=r — радиус конуса.
Рассмотрим прямоугольный треугольник SOB. По свойству биссектрисы треугольника:
![]()

По теореме Пифагора
![]()
Рассмотрим прямоугольный треугольник OO1B.
Сфера и шар Сфера есть множество всех точек пространства, которые находятся на данном расстоянии от данной точки. Точка О называется центром сферы. Любой отрезок, соединяющий центр сферы с какой- либо точкой сферы, называется радиусом сферы(R) Прямая АВ называется осью, а точки А и В пересечения ее со сферой полюсами сферы. Хордой сферы называется отрезок, соединяющий две точки сферы(KN) Диаметром сферы называется хорда, проходящая через ее центр(АВ) R N K

Шар Шаром с центром в точке О и радиуса R называется множество всех точек пространства, находящихся от точки О на расстоянии, не превосходящем R. Шаром называется тело, ограниченное сферой. Шар образуется вращением полукруга около его неподвижного диаметра(АВ) Этот диаметр называется осью шара, а оба конца указанного диаметра полюсами шара. Поверхность шара называется сферой. R A B

Часть шара (сферы), отсекаемая от него какой-либо плоскостью (ABC), называется шаровым сегментом. Круг ABC называется основанием шарового сегмента. Отрезок MN перпендикуляра, проведенного из центра N круга ABC до пересечения со сферической поверхностью, называется высотой шарового сегмента. Точка M называется вершиной шарового сегмента. Шаровой сегмент Формулы: V=1/3П 2 H(3R-H)

Шаровой слой Часть сферы, заключённая между двумя параллельными плоскостями ABC и DEF, пересекающими сферическую поверхность, называется шаровым слоем Кривая поверхность шарового слоя называется шаровым поясом. Круги ABC и DEF – основания шарового пояса. Расстояние NK между основаниями шарового пояса – его высота.



Сфера, вписанная в конас Сфера называется вписанной в конас, если она касается всех образующих конаса и его основания. В любой конас можно вписать сферу. Центр сферы лежит на оси конаса и является центром окружности, вписанной в осевое сечение конаса. Формулы радиуса шара, вписанного в конас: R - радиус вписанного шара, r - радиус основания конаса, l - длина образующей конаса, H - высота конаса, A - угол наклона образующей конаса к его основанию. l H l r Формулы: R=rtgA/2 R=Hr/(l+r) L r R R O1 A A/2


Задача 1 Задача 1. В конас вписан шар радиуса r. Найти объем конаса, если его высота равна h. Решение: Осевое сечение данной комбинации шара и конаса – это равнобедренный треугольник PAB, описанный вокруг окружности с центром О и радиусом R, PC = h – высота конаса, OD PB. Объем конаса Так как поэтому или откуда Следовательно, Ответ:

Задача 2 В шар радиуса R вписан конас, высота которого Н. Найдите угол между образующей конаса и плоскостью основания. Рассмотрим диаметральное сечение шара, как показано на рисунке б). Как известно угол между прямой и плоскостью есть угол между этой прямой и её проекцией на эту плоскость. В нашем случае АВ - прямая, а АР - проекция. ОР=ВР-ОВ=H-R(где H-высота конаса,R-радиус сферы) Из прямоугольного треугольника ОАР определим катет АР по теореме Пифагора: R H Ответ: O

Конас Ко́нас тело, полученное объединением всех лучей, исходящих из одной точки (вершины конаса) и проходящих через плоскую поверхность. Иногда конасом называют часть такого тела, полученную объединением всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае называют основанием конаса, а конас называют опирающимся на данное основание). Если основание конаса представляет собой многоугольник, конас становится пирамидой. Геометрическое тело, создаваемое вращением прямоугольного треугольника вокруг одного из катетов

Элементы и части конаса Вершина точка при неподвижном остром угле вращающегося прямоугольного треугольника, образующего конас. Основание круг, ограничивающий конас, описываемый подвижным катетом образующего треугольника. Высота отрезок, перпендикулярный основанию, проходящий через вершину, неподвижный катет образующего треугольника, а также длина этого отрезка. Образующая отрезок, соединяющий вершину и точку на окружности, ограничивающей основание, гипотенуза описывающего треугольника. Боковая поверхность коническая поверхность, ограничивающая конас, образуемая гипотенузой образующего треугольника. o p БОКОВАЯ ПОВЕРХНОСТЬ ОБРАЗУЮЩАЯ ОСНОВАНИЕ КОНУСА РАДИУС ВЕРШИНА ОСЬ

Усеченный конас Усеченным конасом называют тело вращения, образованное вращением прямоугольной трапеции около боковой стороны, перпендикулярной основаниям. Круги O и O1 - его основания, его образующие AA1 равны между собой, прямая OO1 - ось, отрезок OO1 - высота. Его осевое сечение - равнобедренная трапеция.

Связанные определения Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конаса. Прямая, соединяющая вершину и центр основания, называется осью конаса. Круговой конас конас, основание которого является кругом. Конас, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конасом (последние два имеют бесконечный объём). Часть конаса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конасом.

Конас, вписанный в окружность Шар называется описанным около многогранника, а многогранник вписанным в шар, если поверхность шара проходит через все вершины многогранника. Шар называется описанным около усеченного конаса (конаса), если окружности оснований (окружность основания и вершина)принадлежат поверхности шара. Центр шара, описанного около многогранника, лежит в точке пересечения плоскостей, перпендикулярных ко всем ребрам многогранника и проходящих через их середины. Он может быть расположен внутри, на поверхности и вне многогранника. Конас вписан в сферу (сфера описана около конаса), если его вершина принадлежит сфере, а основание является сечением шара (AOC), ограниченного данной сферой Около конаса всегда можно описать шар. Его центр лежит на оси конаса и совпадает с центром окружности, описанной около треугольника, являющегося осевым сечением конаса. A B AC O Формулы: R 2 =(H-R) 2 +r 2 R-радиус шара r- радиус основания конаса H-высота конаса


Пирамида, вписанная в конус Пирамида называется вписанной в конус, если ее основание вписано в основание конуса, а вершина совпадает с вершиной конуса. При этом конус называется описанным около пирамиды. Пирамида, вписанная в конус Около пирамиды можно описать конус тогда и только тогда, когда около ее основания можно описать окружность. Упражнение 1 Найдите сторону основания правильной треугольной пирамиды, вписанной в конус, радиус основания которого равен 1. Ответ: 3. Упражнение 2 Найдите сторону основания правильной четырехугольной пирамиды, вписанной в конус, диаметр основания которого равен 1. Ответ: 2 2 . Упражнение 3 Найдите сторону основания правильной шестиугольной пирамиды, вписанной в конус, радиус основания которого равен 1. Ответ: 1. Пирамида, описанная около конуса Пирамида называется описанной около конуса, если ее основание описано около основания конуса, а вершина совпадает с вершиной конуса. При этом конус называется вписанным в пирамиду. Пирамида, описанная около конуса В пирамиду можно вписать конус тогда и только тогда, когда в ее основание можно вписать окружность. Упражнение 1 Найдите сторону основания правильной треугольной пирамиды, описанной около конуса, радиус основания которого равен 1. Ответ: 2 3. Упражнение 2 Найдите сторону основания правильной четырехугольной пирамиды, описанной около конуса, радиус основания которого равен 1. Ответ: 2. Упражнение 3 Найдите сторону основания правильной шестиугольной пирамиды, описанной около конуса, радиус основания которого равен 1. Ответ: 2 3 3 . Сфера, вписанная в конус Сфера называется вписанной в конус, если она касается его основания и боковой поверхности (касается каждой образующей). При этом конус называется описанным около сферы. Сфера, вписанная в конус Сфера называется вписанной в конус, если она касается его основания и боковой поверхности (касается каждой образующей). При этом конус называется описанным около сферы. В любой конус (прямой, круговой) можно вписать сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, вписанной в треугольник, являющийся осевым сечением конуса. Напомним, что радиус r окружности, вписанный в треугольник, находится S по формуле r , p где S – площадь, p – полупериметр треугольника. Упражнение 1 В конус, радиус основания которого равен 1, а образующая равна 2, вписана сфера. Найдите ее радиус. Решение. Треугольник SAB равносторонний. Высота SH равна 3 . Площадь S равна Полупериметр p равен 3. По формуле r = S/p получаем r 3 3 . 3. Упражнение 2 В конус, радиус основания которого равен 2, вписана сфера радиуса 1. Найдите высоту конуса. Решение. Обозначим h высоту SH конуса. Из формулы r = S/p имеем: 2 rp h , a где r = 1, a = FG = 4, p = 2 Решая уравнение находим h 8 3 2h 2 . 4 h . 2 4 h , 2 Упражнение 3 Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45о. Найдите радиус вписанной сферы. Решение. Высота SH конуса равна 1. Образующая.2 Полупериметр p равен 1 По формуле r = S/p, имеем r 1 1 Ответ: r 2 1. 2 2 1. 2. Упражнение 4 Высота конуса равна 8, образующая 10. Найдите радиус вписанной сферы. Решение. Радиус основания конуса равен 6. Площадь треугольника SFG равна 48, полупериметр 16. По формуле r = S/p имеем r = 3. Ответ: r = 3. Упражнение 5 Можно ли вписать сферу в наклонный конус? Ответ: Нет. Сфера, вписанная в усеченный конус Сфера называется вписанной в усеченный конус, если она касается его оснований и боковой поверхности (касается каждой образующей). При этом усеченный конус называется описанным около сферы. В усеченный конус можно вписать сферу, если в его осевое сечение можно вписать окружность. Радиус этой окружности будет равен радиусу вписанной сферы. Упражнение 1 В усеченный конус, радиусы оснований которого равны 2 и 1, вписана сфера. Найдите радиус сферы и высоту усеченного конуса. Решение. Имеем: A1B = A1O1= 2, A2B = A2O2= 1. Следовательно, A1A2 = 3, A1C = 1. O 1O 2 A 2 C A1 A 2 A1 C 2 Таким образом, r 2, h 2 2. 2 2 2. Упражнение 2 В усеченный конус, радиус одного основания которого равен 2, вписана сфера радиуса 1. Найдите радиус второго основания. Решение. Пусть A1O1= 2. Обозначим r = A2O2. Имеем: A1A2 = 2+r, A1C = 2 – r. По теореме Пифагора, имеет место равенство O 1 O 2 2 A1 A 2 2 A1 C 2 , из которого следует, что выполняется 2 2 4 (r 2) (2 r) . Решая равенство полученное уравнение относительно r, находим 1 r . 2 Упражнение 3 В усеченном конусе радиус большего основания равен 2, образующая наклонена к плоскости основания под углом 60о. Найдите радиус вписанной сферы. Решение. Заметим, что осевым сечением конуса, из которого получен усеченный конус, является равносторонний треугольник со стороной 2. Радиус r сферы, вписанной в усеченный конус, равен радиусу окружности, вписанной в этот равносторонний треугольник, т.е. 3 r . 3 Упражнение 4 Образующая усеченного конуса равна 2, площадь осевого сечения 3. Найдите радиус вписанной сферы. Решение. Воспользуемся формулой r = S/p, где S – площадь осевого сечения, p – полупериметр. В нашем случае S = 3. Для нахождения полупериметра напомним, что для четырехугольника, описанного около окружности, суммы противоположных сторон равны. Значит, полупериметр равен удвоенной образующей цилиндра, т.е. p = 4. Следовательно, r = ¾. Ответ: r 3 4 . Упражнение 5 Можно ли вписать сферу в усеченный наклонный конус. Ответ: Нет. Сфера, описанная около конуса Сфера называется описанной около конуса, если вершина и окружность основания конуса лежат на сфере. При этом конус называется вписанным в сферу. Сфера, описанная около конуса Около любого конуса (прямого, кругового) можно описать сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, описанной около треугольника, являющимся осевым сечением конуса. Напомним, что радиус R окружности, описанной около треугольника, находится по формуле R a b c , 4S где S – площадь, a, b, c – стороны треугольника. Упражнение 1 Около конуса, радиус основания которого равен 1, а образующая равна 2, описана сфера. Найдите ее радиус. Решение. Треугольник SAB равносторонний со стороной 2. Высота SH равна 3 . Площадь S равна 3 . По формуле R = abc/4S получаем R 2 3 3 . Упражнение 2 Около конуса, радиус основания которого равен 4, описана сфера радиуса 5. Найдите высоту h конуса. Решение. Имеем, OB = 5, HB = 4. Следовательно, OH = 3. Учитывая, что SO = OB = 5, получаем h = 8. Ответ: h = 8. Упражнение 3 Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45о. Найдите радиус описанной сферы. Решение. Треугольник SAB – прямоугольный, равнобедренный. Следовательно, радиус R описанной сферы равен радиусу основания цилиндра, т.е. R = 1. Ответ: R = 1. Упражнение 4 Высота конуса равна 8, образующая 10. Найдите радиус описанной сферы. Решение. В треугольнике SAB имеем: SA = SB = 10, SH = 8. По теореме Пифагора, AH = 6 и, следовательно, S = 48. Используя формулу R = abc/4S, получаем R 25 6 . Упражнение 5 Можно ли описать сферу около наклонного конуса? Ответ: Да. Сфера, описанная около усеченного конуса Сфера называется описанной около усеченного конуса, если окружности оснований усеченного конуса лежат на сфере. При этом усеченный конус называется вписанным в сферу. Около усеченного конуса можно описать сферу, если около его осевого сечения можно описать окружность. Радиус этой окружности будет равен радиусу описанной сферы. Упражнение 1 Около усеченного конуса, радиусы оснований которого равны 2 и 1, а образующая равна 2, описана сфера. Найдите ее радиус. Решение. Заметим, что A1O1B2O2 и O1B1B2A2 – ромбы. Треугольники A1O1A2, O1A2B2, O1B1B2 – равносторонние и, значит, A1B1 – диаметр. Следовательно, R =2. Ответ: R = 2, Упражнение 2 Радиус меньшего основания усеченного конуса равен 1, образующая равна 2 и составляет угол 45о с плоскостью другого основания. Найдите радиус описанной сферы. Решение. Имеем A2O2 = 1, A1A2 = 2, O1O2 = 2 , OO1 = O1C = 1. Следовательно, OO2 = 1 + 2 и, значит, R AO2 4 2 2. Упражнение 3 Радиус одного основания усеченного конуса равен 4, высота 7, радиус описанной сферы 5. Найдите радиус второго основания усеченного конуса. Решение. Имеем OO1 = 3, OO2 = 4 и, следовательно, O2A2 = 3. Ответ: 3. Упражнение 4 Найдите радиус сферы, описанной около усеченного конуса, радиусы оснований которого равны 2 и 4, а высота равна 5. Решение. Обозначим R радиус описанной сферы. Тогда O O1 R 2 4 , OO2 R 2 1. Учитывая, что O1O2 = 6, имеем равенство 5 R 2 4 R 2 1. Решая его относительно R, находим R 221 5 . Упражнение 5 Можно ли описать сферу около усеченного наклонного конуса. Ответ: Нет.
Сфера, вписанная в цилиндр Сфера называется вписанной в цилиндр, если она касается его оснований и боковой поверхности (касается каждой образующей). При этом цилиндр называется описанным около сферы. В цилиндр можно вписать сферу, если высота цилиндра равна диаметру его основания. Ее центром будет точка O, являющаяся серединой отрезка, соединяющего центры оснований O 1 и O 2 цилиндра. Радиус сферы R будет равен радиусу окружности основания цилиндра.













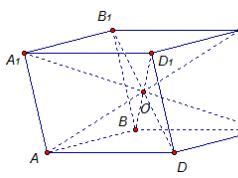
Сфера, описанная около цилиндра Цилиндр называется вписанным в сферу, если окружности оснований цилиндра лежат на сфере. При этом сфера называется описанной около цилиндра. Около любого цилиндра можно описать сферу. Ее центром будет точка O, являющаяся серединой отрезка, соединяющего центры оснований O 1 и O 2 цилиндра. Радиус сферы R вычисляется по формуле где h – высота цилиндра, r – радиус окружности основания.






Цилиндр, вписанный в призму Цилиндр называется вписанным в призму, если его основания вписаны в основания цилиндра. При этом, призма называется описанной около цилиндра В призму можно вписать цилиндр тогда и только тогда, когда в ее основание можно вписать окружность. Радиус основания цилиндра равен радиусу окружности, вписанной в основание призмы. Высота цилиндра равна высоте призмы.






Цилиндр, описанный около призмы Цилиндр называется описанным около призмы, если его основания описаны около оснований цилиндра. При этом, призма называется вписанной в цилиндр Около призмы можно описать цилиндр, если около ее оснований можно описать окружности. Высота цилиндра равна высоте призмы. радиусу окружности, описанной около основания призмы. Радиус основания цилиндра равен